Derivation
Skipping the tedious part of the derivation - very similar to the 1D, except we set $\mathbf E=(0,0,E_z)$ and $\mathbf{\tilde{H}}=(\tilde H_x,\tilde H_y,0)$, since these turn out to be the coupled equations (the other components become a ‘$H_z$’ mode).
The curl equations reduce therefore to:
$$
\frac{\mu}{c_0}\frac{\partial \tilde H_x}{\partial t} = -\frac{\partial E_z}{\partial y}
$$
$$
\frac{\mu}{c_0}\,\frac{\partial \tilde H_y}{\partial t} = \frac{\partial E_z}{\partial x}
$$
$$
\frac{\varepsilon}{c_0}\frac{\partial E_z}{\partial t} = \frac{\partial \tilde H_y}{\partial x} - \frac{\partial \tilde H_x}{\partial y}
$$
And the update equations become:
$$
\begin{align}
\tilde H_x^{i,j+\frac12}\Big(t+\frac{\Delta t}{2}\Big)
&= \tilde H_x^{i,j+\frac12}\Big(t-\frac{\Delta t}{2}\Big)
- \frac{c_0\Delta t}{\mu^{i,j+\frac12}}
\frac{E^{i,j+1}(t)-E^{i,j}(t)}{\Delta y}, \\[6pt]
\tilde H_y^{i+\frac12,j}\Big(t+\frac{\Delta t}{2}\Big)
&= \tilde H_y^{i+\frac12,j}\Big(t-\frac{\Delta t}{2}\Big)
+ \frac{c_0\Delta t}{\mu^{i+\frac12,j}}
\frac{E^{i+1,j}(t)-E^{i,j}(t)}{\Delta x}, \\[6pt]
E^{i,j}(t+\Delta t)
&= E^{i,j}(t)
+ \frac{c_0\Delta t}{\varepsilon^{i,j}}\Bigg(
\frac{\tilde H_y^{i+\frac12,j}\big(t+\frac{\Delta t}{2}\big)-\tilde H_y^{i-\frac12,j}\big(t+\frac{\Delta t}{2}\big)}{\Delta x} \nonumber\\
&\qquad\qquad\qquad\qquad
- \frac{\tilde H_x^{i,j+\frac12}\big(t+\frac{\Delta t}{2}\big)-\tilde H_x^{i,j-\frac12}\big(t+\frac{\Delta t}{2}\big)}{\Delta y}\Bigg)
\end{align}
$$
(thanks ChatGPT).
Implementation
Free Space
Implemented materials, but haven’t added graphics/tested yet:
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as spi
import matplotlib.animation as animation
N = 100 # Grid resolution
X, Y = 1.0, 1.0 # Domain size
dx, dy = X / N, Y / N # Spatial steps
dt = 0.005 # Time step
T = 3.0 # Total time
c0 = 1.0 # Speed of light
rec_interval = 2 # Snapshot interval for animation
Hx, Hy = np.zeros((N, N-1)), np.zeros((N-1, N)) # Magnetic fields
Ez = np.zeros((N, N)) # Electric field
def create_gaussian_pulse(cx, cy, r, A=1.0):
x = np.linspace(0, X, N)
y = np.linspace(0, Y, N)
X_grid, Y_grid = np.meshgrid(x, y)
return A * np.exp(-((X_grid - cx)**2 + (Y_grid - cy)**2) / (2 * r**2))
Ez = create_gaussian_pulse(X/4, Y/4, 0.05, 1.0)
eps = np.ones((N, N)) # Permittivity
mu = np.ones((N, N)) # Permeability
def create_material(x0, x1, y0, y1, permittivity=1.0, permeability=1.0):
global eps, mu
i0 = int(np.floor(x0 / dx)); i1 = int(np.ceil(x1 / dx))
j0 = int(np.floor(y0 / dy)); j1 = int(np.ceil(y1 / dy))
i0, i1 = max(0, i0), min(N, i1)
j0, j1 = max(0, j0), min(N, j1)
eps[i0:i1, j0:j1] = permittivity
mu[i0:i1, j0:j1] = permeability
MATERIALS = [
# (0.4, 0.6, 0.4, 0.6, 4.0, 1.0),
]
for mat in MATERIALS:
create_material(*mat)
# Compute average mu for H positions
mu_x = 0.5 * (mu[:, :-1] + mu[:, 1:])
mu_y = 0.5 * (mu[:-1, :] + mu[1:, :])
h_coeff_x = c0*dt/mu_x # Update coefficients for Hx
h_coeff_y = c0*dt/mu_y # Update coefficients for Hy
e_coeff = c0*dt/eps # Update coefficients for E
def update(half_step):
global Hx, Hy, Ez
if half_step:
Hx += -h_coeff_x * (Ez[:, 1:] - Ez[:, :-1]) / dy
Hy += h_coeff_y * (Ez[1:, :] - Ez[:-1, :]) / dx
else:
Ez[1:-1, 1:-1] += e_coeff[1:-1, 1:-1] * (
(Hy[1:, 1:-1] - Hy[:-1, 1:-1]) / dx -
(Hx[1:-1, 1:] - Hx[1:-1, :-1]) / dy
)
Ez[0, :] = Ez[-1, :] = Ez[:, 0] = Ez[:, -1] = 0.0 # Dirichlet BC
def run_simulation(steps):
global Hx, Hy, Ez, MATERIALS
hist_Hx, hist_Hy, hist_Ez = [], [], []
hist_Hx.append(Hx.copy())
hist_Hy.append(Hy.copy())
hist_Ez.append(Ez.copy())
for step in range(steps):
update(1) # Half-step for H
update(0) # Full-step for E
if (step+1) % rec_interval == 0:
hist_Hx.append(Hx.copy())
hist_Hy.append(Hy.copy())
hist_Ez.append(Ez.copy())
return hist_Hx, hist_Hy, hist_Ez
def center_H(Hx, Hy):
Hx_c = np.zeros((N, N))
Hy_c = np.zeros((N, N))
if N > 2: Hx_c[:, 1:-1] = 0.5 * (Hx[:, 1:] + Hx[:, :-1])
Hx_c[:, 0] = Hx[:, 0]; Hx_c[:, -1] = Hx[:, -1]
if N > 2: Hy_c[1:-1, :] = 0.5 * (Hy[1:, :] + Hy[:-1, :])
Hy_c[0, :] = Hy[0, :]; Hy_c[-1, :] = Hy[-1, :]
return Hx_c, Hy_c
def visualise(hist_Hx, hist_Hy, hist_Ez, show_H=False, save=False):
fig, ax = plt.subplots()
Xc, Yc = np.meshgrid(np.arange(N) * dx + 0.5 * dx, np.arange(N) * dy + 0.5 * dy)
im = ax.imshow(hist_Ez[0].T, origin='lower', extent=(0, X, 0, Y),
cmap='RdBu', vmin=-1.0, vmax=1.0, interpolation='bilinear', zorder=1)
quiv = None
if show_H:
quiver_scale = 10.0
quiver_width = 0.002
quiver_color = (0, 0, 0, 0.5)
Hx_c0, Hy_c0 = center_H(hist_Hx[0], hist_Hy[0])
quiv = ax.quiver(Xc, Yc, Hx_c0.T, Hy_c0.T,
scale=quiver_scale, pivot='mid', width=quiver_width, color=quiver_color, zorder=3)
ax.set_xlabel('x'); ax.set_ylabel('y')
ax.set_title('2D FDTD Simulation')
ax.set_xlim(0, X); ax.set_ylim(0, Y)
cb = plt.colorbar(im, ax=ax, fraction=0.046, pad=0.04)
time_text = ax.text(0.02, 0.95, '', transform=ax.transAxes, color='k')
def animate(i):
im.set_array(hist_Ez[i].T)
if show_H:
Hx_c, Hy_c = center_H(hist_Hx[i], hist_Hy[i])
quiv.set_UVC(Hx_c.T, Hy_c.T)
time_text.set_text(f't = {i * dt:.4f}s')
return [im, time_text] + ([quiv] if show_H else [])
ani = animation.FuncAnimation(fig, animate, frames=len(hist_Ez), interval=10, blit=True)
if save:
ani.save('output.gif', writer='ffmpeg', fps=30)
plt.show()
hist_Hx, hist_Hy, hist_Ez = run_simulation(int(T/dt))
visualise(hist_Hx, hist_Hy, hist_Ez, show_H=True, save=True)
Creates the given output:
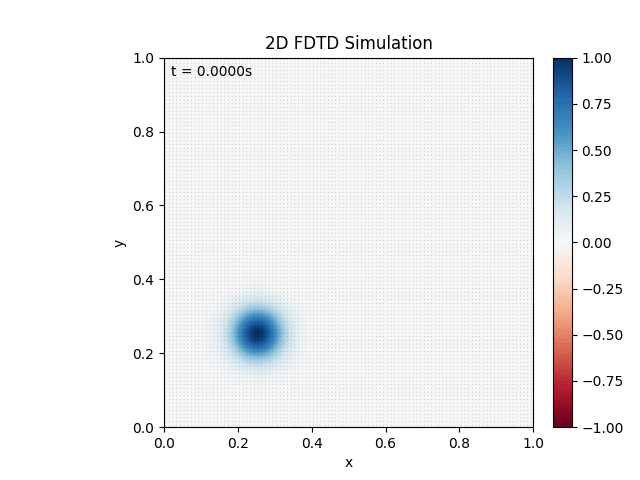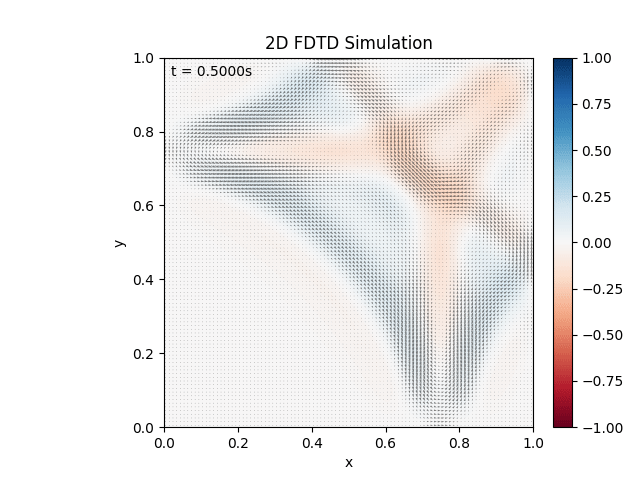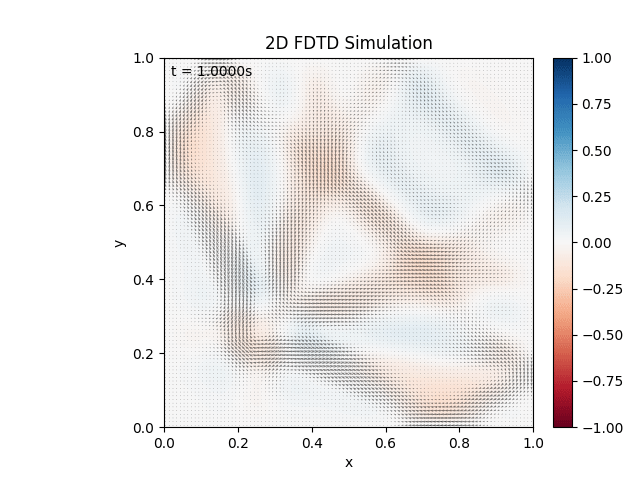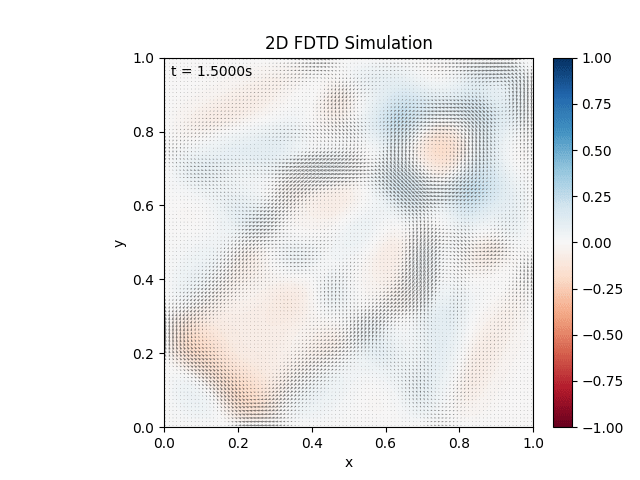
I’m pretty happy with this. $dt$ needs to be smaller to satisfy the CFL convergence condition. The black ‘dots’ are the magnetic field rendered as a vector field, just really small.
Materials Testing
Not actually sure what happened, but turns out a lot of transpose/x/y things screwed up, so half the things (waves, etc.) were flipped while some other things (materials) rendered normally (i.e. not mirrored along $y=x$).
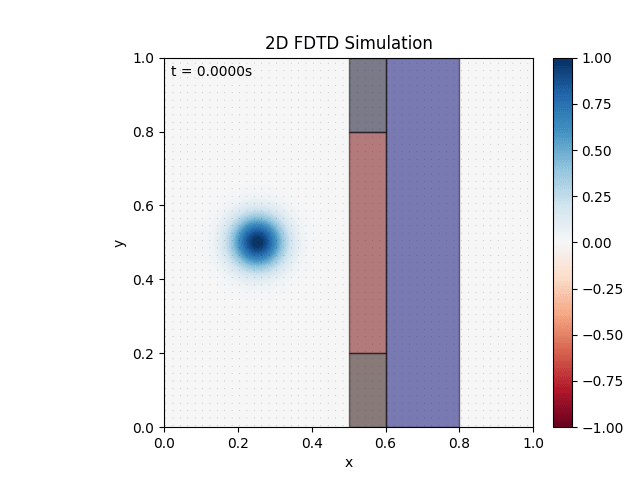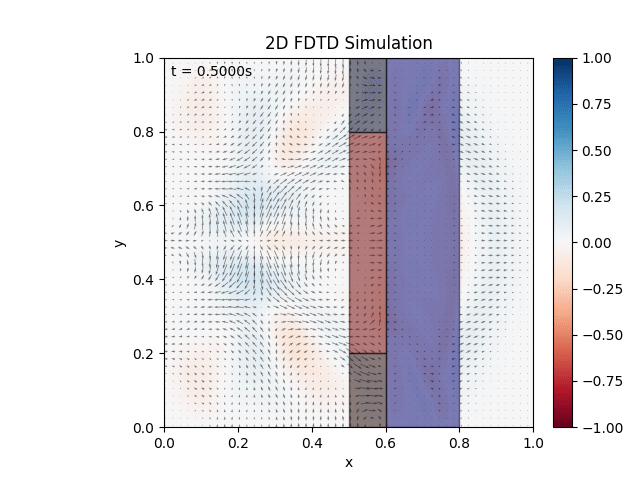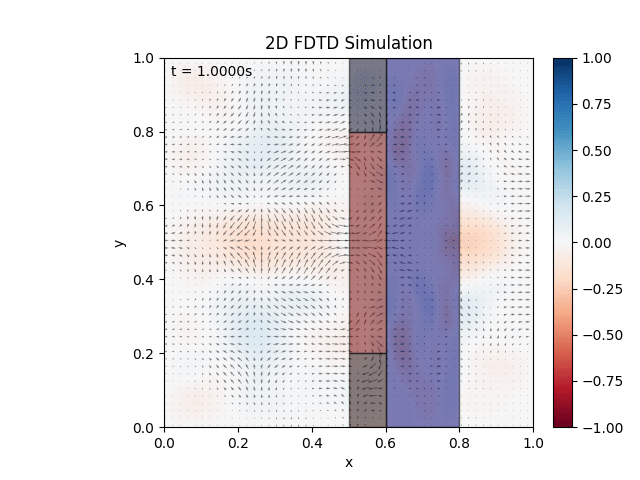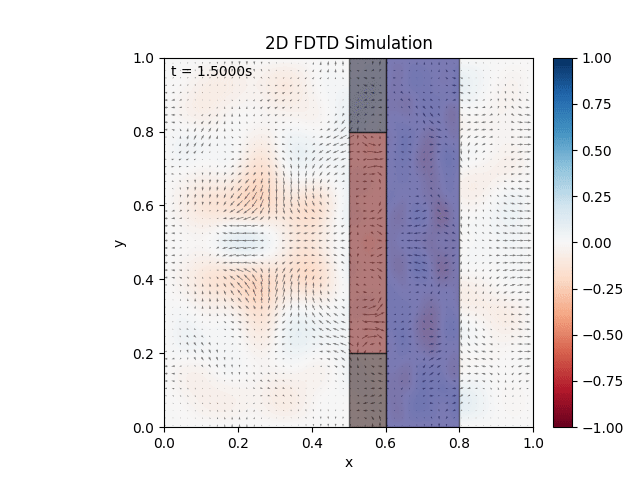
Either way, cleared up the mishap, adjusted visuals, and tested a material:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import Rectangle
N = 100 # Grid resolution
X, Y = 1.0, 1.0 # Domain size
dx, dy = X / N, Y / N # Spatial steps
dt = 0.005 # Time step
T = 3.0 # Total time
c0 = 1.0 # Speed of light
rec_interval = 2 # Snapshot interval for animation
Hx, Hy = np.zeros((N, N-1)), np.zeros((N-1, N)) # Magnetic fields
Ez = np.zeros((N, N)) # Electric field
def create_gaussian_pulse(cx, cy, r, A=1.0):
x = np.linspace(0, X, N)
y = np.linspace(0, Y, N)
X_grid, Y_grid = np.meshgrid(x, y)
return A * np.exp(-((X_grid - cx)**2 + (Y_grid - cy)**2) / (2 * r**2))
Ez = create_gaussian_pulse(X/4, Y/2, 0.05, 1.0)
eps = np.ones((N, N)) # Permittivity
mu = np.ones((N, N)) # Permeability
def create_material(x0, x1, y0, y1, permittivity=1.0, permeability=1.0):
global eps, mu
i0 = int(np.floor(x0 / dx)); i1 = int(np.ceil(x1 / dx))
j0 = int(np.floor(y0 / dy)); j1 = int(np.ceil(y1 / dy))
i0, i1 = max(0, i0), min(N, i1)
j0, j1 = max(0, j0), min(N, j1)
eps[j0:j1, i0:i1] = permittivity
mu[j0:j1, i0:i1] = permeability
MATERIALS = [
(0.6, 0.7, 0.2, 0.8, 5.0, 1.0)
]
for mat in MATERIALS:
create_material(*mat)
# Compute average mu for H positions
mu_x = 0.5 * (mu[:, :-1] + mu[:, 1:])
mu_y = 0.5 * (mu[:-1, :] + mu[1:, :])
h_coeff_x = c0*dt/mu_x # Update coefficients for Hx
h_coeff_y = c0*dt/mu_y # Update coefficients for Hy
e_coeff = c0*dt/eps # Update coefficients for E
def update(half_step):
global Hx, Hy, Ez
if half_step:
Hx += -h_coeff_x * (Ez[:, 1:] - Ez[:, :-1]) / dy
Hy += h_coeff_y * (Ez[1:, :] - Ez[:-1, :]) / dx
else:
Ez[1:-1, 1:-1] += e_coeff[1:-1, 1:-1] * (
(Hy[1:, 1:-1] - Hy[:-1, 1:-1]) / dx -
(Hx[1:-1, 1:] - Hx[1:-1, :-1]) / dy
)
Ez[0, :] = Ez[-1, :] = Ez[:, 0] = Ez[:, -1] = 0.0 # Dirichlet BC
def run_simulation(steps):
global Hx, Hy, Ez, MATERIALS
hist_Hx, hist_Hy, hist_Ez = [], [], []
hist_Hx.append(Hx.copy())
hist_Hy.append(Hy.copy())
hist_Ez.append(Ez.copy())
for step in range(steps):
update(1) # Half-step for H
update(0) # Full-step for E
if (step+1) % rec_interval == 0:
hist_Hx.append(Hx.copy())
hist_Hy.append(Hy.copy())
hist_Ez.append(Ez.copy())
return hist_Hx, hist_Hy, hist_Ez
def center_H(Hx, Hy):
Hx_c = np.zeros((N, N))
Hy_c = np.zeros((N, N))
if N > 2: Hx_c[:, 1:-1] = 0.5 * (Hx[:, 1:] + Hx[:, :-1])
Hx_c[:, 0] = Hx[:, 0]; Hx_c[:, -1] = Hx[:, -1]
if N > 2: Hy_c[1:-1, :] = 0.5 * (Hy[1:, :] + Hy[:-1, :])
Hy_c[0, :] = Hy[0, :]; Hy_c[-1, :] = Hy[-1, :]
return Hx_c, Hy_c
def visualise(hist_Hx, hist_Hy, hist_Ez, show_H=False, save=False):
fig, ax = plt.subplots()
Xc, Yc = np.meshgrid(np.arange(N) * dx + 0.5 * dx, np.arange(N) * dy + 0.5 * dy)
# Material plots
mat_rects = []
for mat in MATERIALS:
rect = ax.fill_between([mat[0], mat[1]], mat[3], mat[2], color=(abs(mat[4]-1)/9, 0, abs(mat[5]-1)/9, 0.5), edgecolor='k', linewidth=1.0, alpha=0.5, zorder=5)
mat_rects.append(rect)
# E and H plots
im = ax.imshow(hist_Ez[0], origin='lower', extent=(0, X, 0, Y),
cmap='RdBu', vmin=-1.0, vmax=1.0, interpolation='bilinear', zorder=1)
quiv = None
if show_H:
quiver_scale = 5.0
quiver_width = 0.002
quiver_color = (0, 0, 0, 0.5)
Hx_c0, Hy_c0 = center_H(hist_Hx[0], hist_Hy[0])
quiv = ax.quiver(Xc[::2, ::2], Yc[::2, ::2],
Hx_c0[::2, ::2], Hy_c0[::2, ::2],
scale=quiver_scale, pivot='mid', width=quiver_width, color=quiver_color, zorder=3)
ax.set_xlabel('x'); ax.set_ylabel('y')
ax.set_title('2D FDTD Simulation')
ax.set_xlim(0, X); ax.set_ylim(0, Y)
cb = plt.colorbar(im, ax=ax, fraction=0.046, pad=0.04)
time_text = ax.text(0.02, 0.95, '', transform=ax.transAxes, color='k')
def animate(i):
im.set_array(hist_Ez[i])
if show_H:
Hx_c, Hy_c = center_H(hist_Hx[i], hist_Hy[i])
quiv.set_UVC(Hx_c[::2, ::2], Hy_c[::2, ::2])
time_text.set_text(f't = {i * dt:.4f}s')
return [im, time_text, *mat_rects] + ([quiv] if show_H else [])
ani = animation.FuncAnimation(fig, animate, frames=len(hist_Ez), interval=10, blit=True)
if save:
ani.save('output.gif', writer='ffmpeg', fps=30)
plt.show()
hist_Hx, hist_Hy, hist_Ez = run_simulation(int(T/dt))
visualise(hist_Hx, hist_Hy, hist_Ez, show_H=True, save=True)
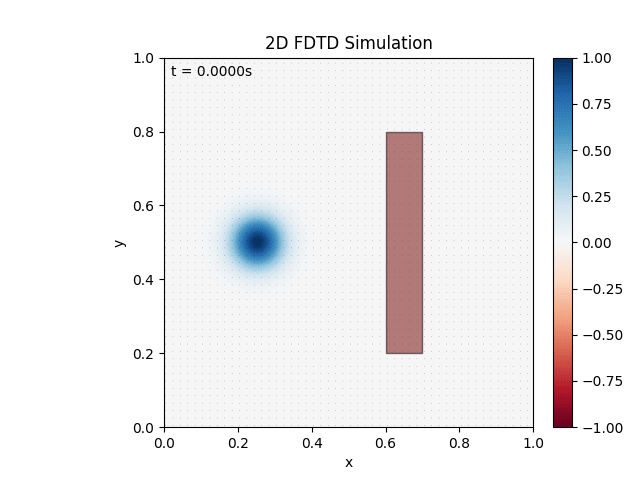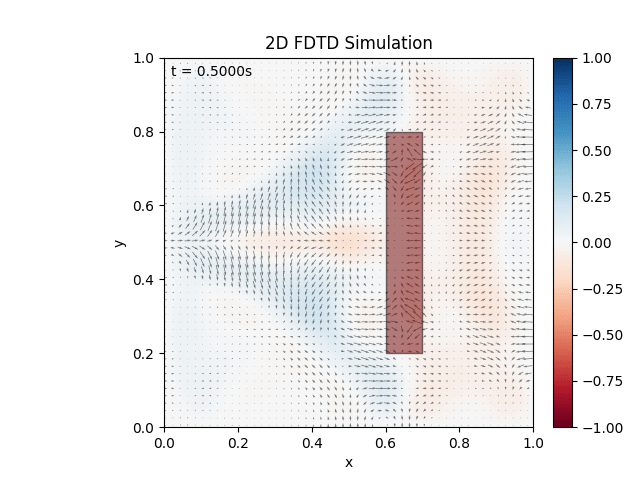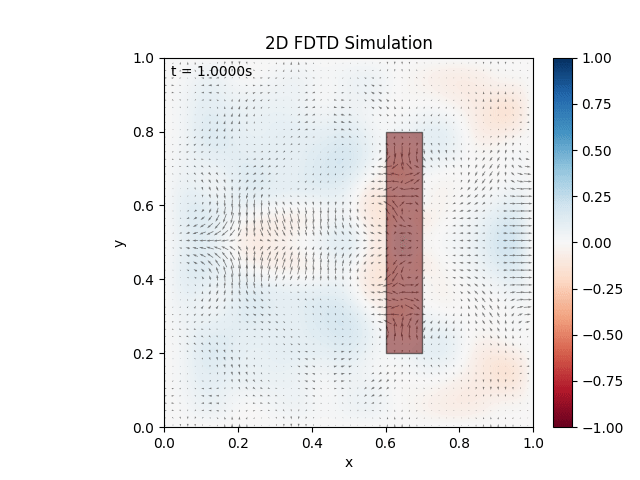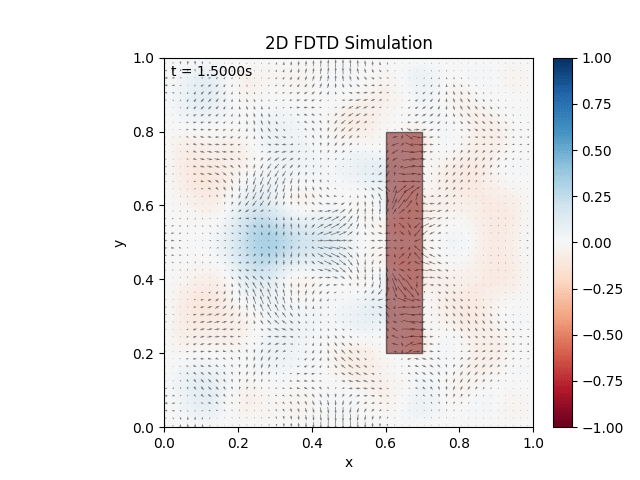
Seems to be working as expected. Testing combination of materials:
