Explanation

Literally just geometry. Like draw crap and good luck. These don’t solve new problems, but give a nicer visualisation.

Here and Now

In a Minkowski diagram when boosting into $S'$, draw the $x'$ and $t'$ axes superimposed on the $S$ basis; allows for understanding:

  1. $t'$ axis makes an angle $\theta$ with $t$ axis such that $\tan\theta=v$.
  2. $x'$ axis is the “now” line of $S'$ - all events in $S$ collinear to a line $y=vx+k$ for some $k\in\mathbb R$ (i.e. parallel to $x'$ axis) happen simultaneously in $S'$.
  3. $t'$ axis is the “here” line of $S'$ - all events in $S$ collinear to a line $y=\frac{1}{v}x+k$ for some $k\in\mathbb R$ (i.e. parallel to $t'$ axis) happen at the same location in $S'$.
  4. Also to be noted that $\frac{\text{len}(x')}{\text{len}(x)}=\sqrt{\frac{1+v^2}{1-v^2}}$ - i.e. as seen in a Minkowski diagram $S$, the length of one unit of $x'$ if drawn on the $S$ diagram is $\sqrt{\frac{1+v^2}{1-v^2}}$ times the length of one unit of $x$ (assume 1).

Problems

Length Contraction

Consider frame $S$ where $S'$ moves towards positive x-axis with speed $v$. Solve with Minkowski diagram with orthogonal $x$ and $t$ axes (i.e. in $S$’s frame): a) Place a meter ruler at rest in $S$. What is its length as measured by $S'$? b) Place a meter ruler at rest in $S'$. What is its length as measured by $S$?

Solution

a) Diagram below:

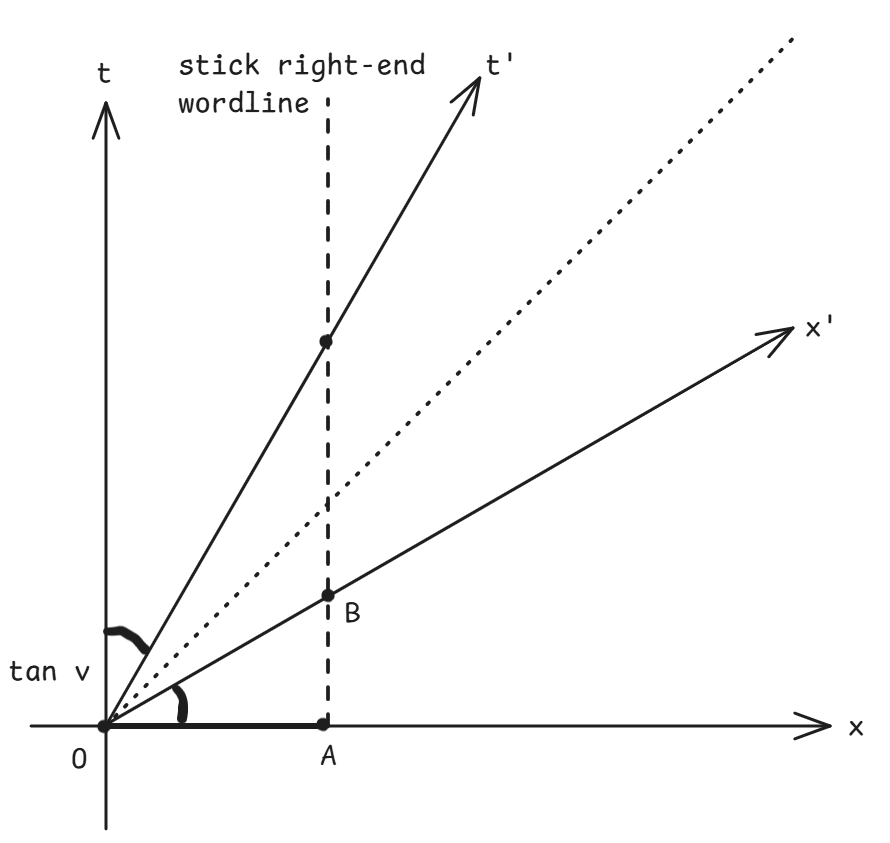
length_cont_minkowski.png

The length of the stick in $S'$ is related to the distance $OB$. With simple geometry, $OB=\sqrt{1+v^2}$ (noting $OA=1$). Therefore, the length $L'$ of the stick in $S'$ is given by

$$L'= \sqrt{1+v^2} \cdot \left( \frac{1+v^2}{1-v^2} \right)^{-1}=\sqrt{1-v^2}=\gamma^{-1}$$

as desired. b) Diagram below:

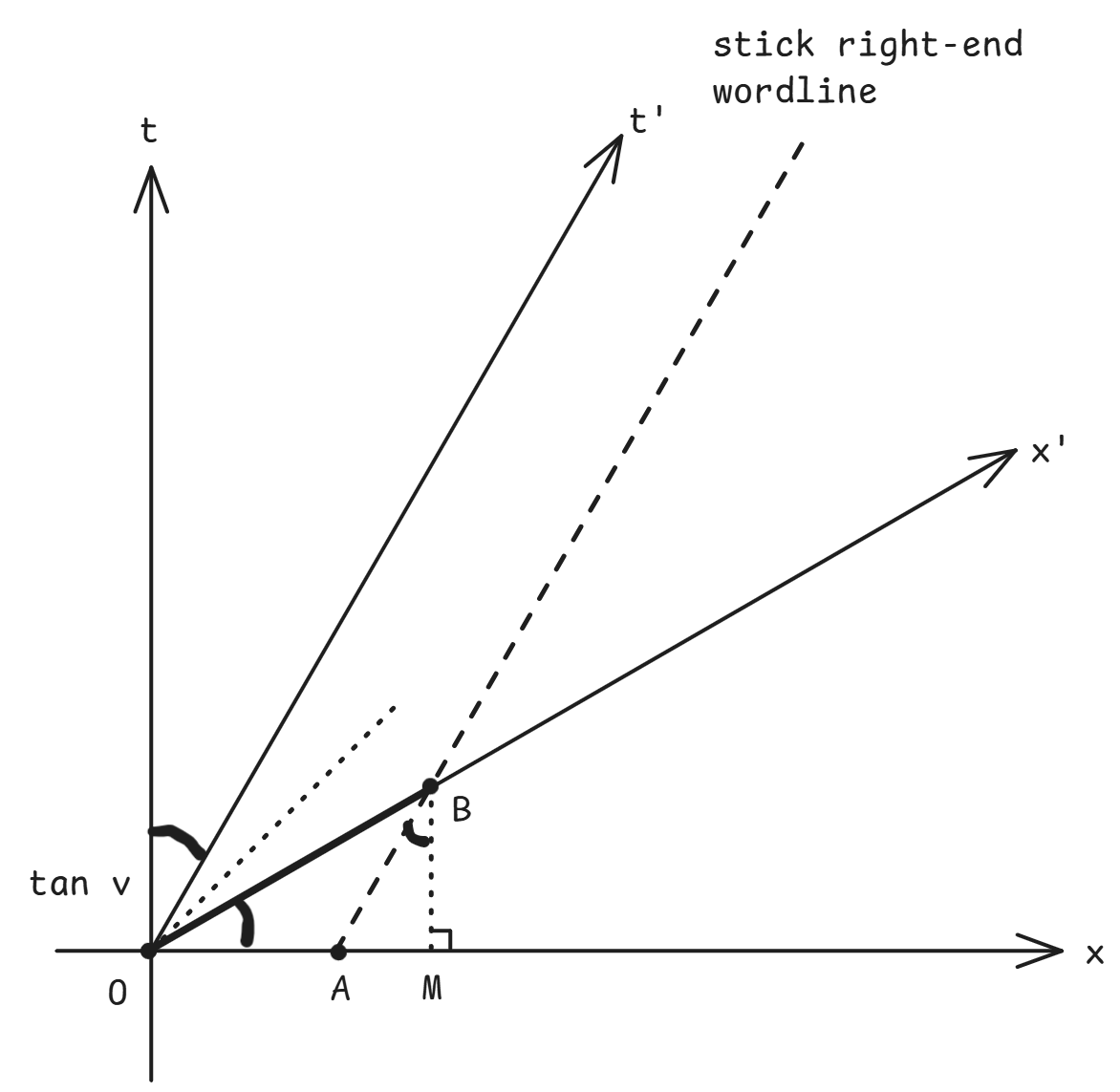
length_cont_2_minkowski.png

The problem is now to find $OA$ given that $OB$ has length $\sqrt{\frac{1+v^2}{1-v^2}}$ on paper. The geometry is fairly straightforward, obtaining $OA=\sqrt{1-v^2}=\gamma^{-1}$, which agrees with the standard result.

Twin Paradox II

The same twin paradox setup, but solve it geometrically with a Minkowski diagram.

Solution
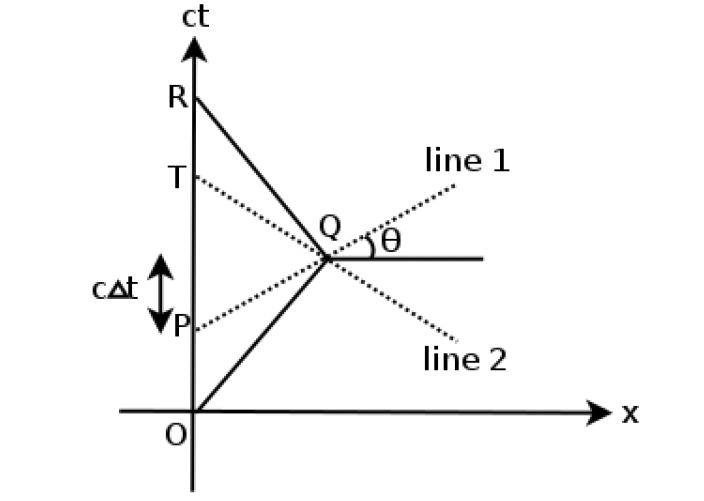
twin_minkowski.png

Consider the problem in the frame of $A$ (the person at rest relative to planet). Person $B$’s worldlines are shown, with line 1 parallel to ‘away-travelling’ x-axis (call this frame $B_1$), and line 2 parallel to ‘toward-travelling’ x-axis (call this frame $B_2$). Events on these lines are simultaneous in $B$’s two frames. In this diagram, it is easy to see that $B$ observes the instantaneous aging of $A$ when they turn - specifically by $2\Delta t$. By simple geometry $\tan \theta = \beta_{B_1}$ and, using proper length in $A$, $\overrightarrow{PQ}_x=L$, so

$$\frac{PT}{2}=c\Delta t=\beta L = \frac{Lv}{c} \implies 2\Delta t=\frac{2Lv}{c^2}$$

Hence, in $B$’s frame, at meetup, $B$’s clock reads $\dfrac{2L}{\gamma v}$, while $A$’s clock reads $\dfrac{2L}{\gamma^2 v}+\dfrac{2Lv}{c^2}=\dfrac{2L}{v}$ as expected (less time has elapsed on $B$’s clock than $A$’s clock).

Streetlamps

In the lab frame $S$, three lamps at coordinates $x_1,x_2,x_3$ are observed to be illuminated at times $t_1,t_2,t_3$. At $t=0$ in $S$, a car is observed to travel from the origin at a constant velocity $v > 0$ in the positive x-direction. a) Under what conditions will the car observe all three lamps to be lit up simultaneously? b) Assume the car observes the events to occur at $t'=0$ in his own frame $S'$. Let the time intervals between the illumination of the lamps and the receipt of the corresponding photons be $\Delta t_1, \Delta t_2, \Delta t_3$ in $S'$. If the car observes $\Delta t_1:\Delta t_2 : \Delta t_3=1:2:3$, determine $x_2,x_3,t_1,t_2,t_3$ in terms of $x_1, v, c$.

Solution

I’m so not bothered to write a solution it’s pretty simple ($x_2=2x_1,x_3=3x_1$ etc.)

Diverging Cars

In lab frame $S$, car 1 travels $v_1=\tan15\degree$ (natural units) in the negative x-direction and car 2 travels $v_2=\frac{1}{\sqrt3}$ in the positive x-direction. Both cars start at $x=0$ at $t=0$ in lab frame. After some time, car 1 emits a light signal in the positive x-direction. Car 1 measures the time interval between itself sending and car 2 receiving to be $t'$. Determine the distance car 2 has travelled in lab frame when it receives the signal.

Solution

Ong not deep.