Minkowski Distance

Distance on the Minkowski diagram (using $x$ and $ct$ axes) is given by

$$(\Delta s)^2=(c\Delta t)^2-(\Delta x)^2$$

and is invariant on hyperbolic rotation. An analogy is the Euclidean metric, where distance is measured as

$$(\Delta s)^2=(\Delta x)^2+(\Delta y)^2$$

and is invariant on circle (?) rotation. Turns out Minkowski spaces and Lorentz transforms have a lot to do with hyperbolic geometry (e.g. events in frame $S'$ trace out a hyperbola in frame $S$ when varying $\gamma_{S'}$, rapidity defined via $\tanh \phi = \beta$ comes with nice properties, etc.)

Proof

Can be proved by just inserting a dummy Lorentz transform (i.e. a hyperbolic rotation). Natural units are adopted and $\Delta$ is dropped for notational convenience ($s^2=x^2-t^2$):

$$ \begin{align} s^2&=-x^2+t^2\\ &=-\gamma^2(x'+vt')^2+\gamma^2(vx'+t')^2\\ &=\gamma^2(-(x')^2-2vx't'-(vt')^2+(vx')^2+2vx't'+(t')^2)\\ &=\gamma^2(-(1-v^2)(x')^2+(1-v^2)(t')^2)\\ &=-(x')^2+(t')^2 = (s')^2 \end{align} $$

as desired.

The three dimensional invariant interval (space-time interval) is given by

$$s^2=t^2-x^2-y^2-z^2$$

omitting $\Delta$. Generally, the metric is called the Minkowski metric,

$$(\eta)_{\alpha \beta} \equiv\begin{bmatrix}-1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{bmatrix}$$

where $x^0\coloneqq t,(x^1,x^2,x^3)\coloneqq (x,y,z)$.

Corollaries

Characterisation of Event Pairs

For some reason textbooks look at these three regions below:

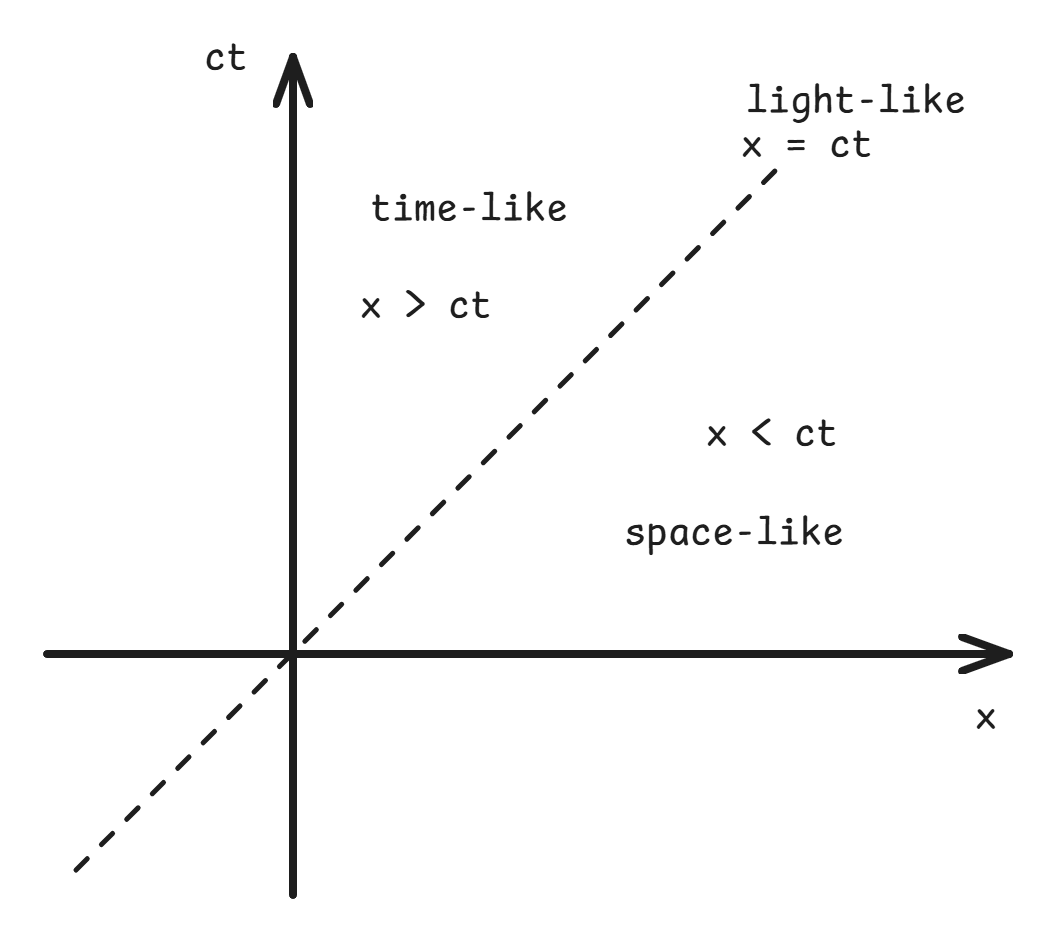
separation_invariant.png

Pretty much if you set the origin to be an event, you can characterise any other event as time-like separated ($(\Delta s)^2>0$), space-like separated ($(\Delta s)^2<0$), or light-like separated ($(\Delta s)^2=0$).

Time-Like ($s^2 > 0$)

When $s^2>0$, $x^2<(ct)^2$, or more intuitively, $\left| \frac{x}{t} \right|<c$. This means that there exists a frame $S'$ which can move at a valid speed $v < c$ such that the two events happen at the same location in $S'$. This statement is equivalent to saying there is a line with slope $>1$ which passes through both points in $S$ (the line corresponds to a vertical line in $S'$).

When $x'=0$ (i.e. in said frame $S'$ which sees the events at the same location),

$$s^2=(ct')^2-(x')^2=(ct')^2\implies ct'=|s|=\sqrt{s^2}$$

so the time separation between the events is $\frac{|s|}{c}$. This is the proper time between the events, since it is observed stationary in a frame.

Space-Like ($s^2<0$)

How can $s^2 < 0$? I guess $s\in \mathbb C$ now. Either way, it means $\left|\frac{x}{t}\right|>c$. This means there exists a frame $S'$ which can move at $v < c$ such that the two events happen simultaneously in $S'$. This statement is equivalent to saying there is a line with slope $< 1$ which passes through both points in $S$ (corresponding to horizontal line in $S'$).

When $t'=0$ (i.e. in said frame $S'$ which sees the events simultaneously),

$$s^2=(ct')^2-(x')^2=-(x')^2\implies x'=|s|=\sqrt{-s^2}$$

so the spatial separation between the events is the magnitude of complex number $s$. This is the proper length, since it is observed in a frame of simultaneity (i.e. it lies on the x axis).

Light-Like ($s^2=0$)

It’s separated like light. $\left|\frac{x}{t}\right|=c$. There are no frames $S'$ where $x'=0$ or $t'=0$ since that would imply $v=c$.

Proper Time, Properly

For a set of time-like separated events with spacetime interval $\Delta s$, proper time can be measured as $c\Delta\tau=|\Delta s'|=|\Delta s|$, where $s'$ is the spacetime interval in a “here” frame. Can figure out proper time for a general object by adding small ‘bits’ of it along an object’s worldline (treating it as a set of events). Specifically,

$$ \begin{align} (ds)^2&=(c\cdot dt)^2-(dx)^2 \\ \implies c^2(d\tau)^2 &= (c\cdot dt)^2-(dx)^2 \end{align} $$

so naturally

$$d\tau=\sqrt{\frac{c^2-\frac{dx}{dt}}{c^2}}\,dt=\sqrt{1-\frac{v^2}{c^2}}\,dt=\frac{dt}{\gamma} \implies \tau=\int \frac{\mathrm{d}t}{\gamma}$$

which is pretty cool.

Problems

Twin Paradox III

Literally the exact same setup again, but solve it by considering the spacetime interval.

Solution

Can use the spacetime interval to derive the proper time formulation above - in which case the problem becomes trivial -

$$t_A=\frac{2L}{v},\, t_B= \tau_B = \int_0^{\frac{L}{v}}\frac{\mathrm dt}{\gamma}+\int_{\frac{L}{v}}^{\frac{2L}{v}}\frac{\mathrm dt}{\gamma}=\frac{2L}{\gamma}=\frac{t_A}{\gamma}$$

Cooked Particle

The velocity of a particle along 1D is given by

$$u(t)=\sqrt{1-\frac{1}{\left(kt+1 \right)^2}}$$

(natural units). Find the proper time of the particle as a function of lab time - i.e. $\tau(t)$, and the position of the particle (in lab frame) as a function of its proper time - i.e. $x(\tau)$.

Solution
$$\frac{1}{\gamma(t)}= \frac{1}{kt+1} \implies \tau = \int \frac{\mathrm dt}{kt+1}=\boxed{\ln|kt+1|}$$

since at $t=0,\tau=0$. Furthermore,

$$ \begin{align} x(t)&=\int_0^t u(t') \,\mathrm dt' \\ &=\int_0^t \sqrt{1-\frac{1}{(kt+1)^2}}\,\mathrm dt \\ &=\frac{1}{k}\left(\sqrt{(kt+1)^2-1}-\sec^{-1}(kt+1)\right) \\ \implies x(\tau)&=\boxed{\frac{1}{k}\left(\sqrt{e^{2k\tau}-1}-\tan^{-1}\sqrt{e^{2k\tau}-1}\right)} \end{align} $$